Chad provides a thorough lesson on Mirrors that includes both plane mirrors and spherical mirrors (both concave and convex mirrors). The lesson begins with plane mirrors (a.k.a. flat mirrors). For a plane mirror a virtual, upright image is located behind the mirror. The image distance is equal to the object distance, and therefore the magnification is equal to 1.

A real image is the result of the reflected rays intersecting at a common point. A virtual image results when the reflected rays do not intersect at all, but appear to have originated from a common point behind the mirror. Images may also be either upright or inverted as well, and for images resulting from a single mirror, real images are always inverted, and virtual images are always upright.
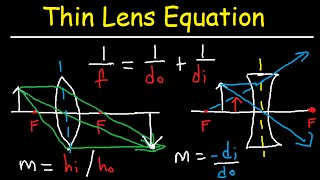
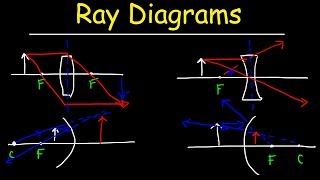
Concave mirrors (sometimes referred to as converging mirrors) are covered next and the focal distance (a.k.a. focal length) is defined as 1/2 the radius of curvature of the mirror. It is the point at which the reflected rays coming from an object infinitely far away from a mirror intersect. Chad also introduces the mirror equation: 1/p + 1/q = 1/f for which p is defined as the object distance, and q as the image distance. He shows that for a concave mirror, there are two possible scenarios. If an object is located further than the focal distance, then a real, inverted image results. If an object is located closer than the focal distance, then a virtual, upright image results. Chad shows how to draw 3 different incident and reflected rays in order to construct a proper ray diagram, and how this ray diagram can be used to understand why and when an image is either real and inverted or virtual and upright.

Next, convex mirrors (sometimes referred to as diverging mirrors) are covered. Chad explains that the focal distance is negative for a convex mirror and must be plugged into the mirror equation as a negative number. He also demonstrates how to draw the 3 rays for a proper ray diagram, and shows that the image resulting from a convex mirror will always be virtual and upright regardless of how close or far an object is placed from the convex mirror.

Chad concludes the lesson by solving several Mirrors calculations involving the mirror equation as well as the magnification equation.

00:00 Lesson Introduction
00:51 Plane Mirrors
05:42 Concave Mirrors
23:01 Convex Mirrors
27:08 Mirrors Problems (Using the Mirror Equation and Magnification)

Check out Chad's General Physics Master Course: https://courses.chadsprep.com/courses...